Si on met en communications deux ballons de baudruche inégalement gonflés, est-ce que c’est le plus gros des ballons qui va se dégonfler dans le plus petit, ou le contraire ? Prenez les paris.
Fiche d’accompagnement de l’expérience:

 Matériel
Matériel-
2 ballons de baudruche ;
-
un petit tube étroit, par exemple un morceau de tuyau ou un tube de carton ;
-
des trombones de bureau ou des pinces à linge ;
-
de l’eau savonneuse ;
-
éventuellement un robinet à 3 voies.
 Montage et réalisation
Montage et réalisationGonfler un ballon de baudruche jusqu’à une taille moyenne et en gonfler un deuxième moins complètement (le deuxième est donc plus petit). Ne pas fermer les ballons par un nœud, tordre seulement l’embouchure et la bloquer par un trombone ou une pince à linge pour empêcher l’air de s’échapper. Raccorder les ballons en retournant les embouchures sur les extrémités d’un petit tube de jonction. Enlever les trombones afin que les ballons communiquent : l’air du plus petit ballon passe dans le plus grand jusqu’à ce que le petit ballon soit pratiquement dégonflé. Si les tailles initiales des ballons ne sont pas celles que nous venons d’indiquer, il peut arriver que les tailles des ballons restent inchangées ou que le gros ballon se dégonfle au profit du plus petit.
Dans le cas où l’on remplace les ballons par des bulles de savon, c’est toujours la plus petite bulle qui disparaît. Plonger deux extrémités d’un robinet à trois voies dans l’eau savonneuse (réserver la troisième comme embouchure pour souffler). Tourner le robinet pour mettre en communication l’embouchure et une autre extrémité puis souffler dans l’embouchure pour faire une bulle à l’extrémité ouverte. Tourner alors le robinet pour faire communiquer l’embouchure avec l’autre extrémité et souffler pour y faire apparaître une deuxième bulle un peu plus grosse que la première. Tourner le robinet pour mettre en communication les deux bulles (embouchure fermée) : c’est la plus petite bulle qui se dégonfle dans la plus grosse. Il faut utiliser une eau savonneuse permettant de faire de grosses bulles qui tiennent longtemps sans éclater, sans quoi l’expérience est délicate. Nous donnons des recettes de solutions savonneuses permettant de faire de grosses bulles qui durent longtemps dans l’expérience de mécanique des liquides « Faire des bulles de savon géantes ».
 Explications
ExplicationsPour expliquer l’expérience avec les bulles de savon il faut s’intéresser à la tension superficielle. Considérons un élément de surface de la bulle de savon
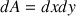
de rayon  (voir la figure 1).
(voir la figure 1).
Les deux côtés 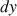 subissent de la part du reste de la bulle des forces de tension superficielle
subissent de la part du reste de la bulle des forces de tension superficielle 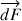 et
et 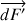 de valeur commune
de valeur commune
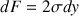
(le facteur 2 est dû au fait que la pellicule d’eau savonneuse est constituée de 2 interfaces eau-air, l’une à l’intérieur et l’autre à l’extérieur). On a :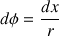
( 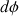 : angle sous lequel on voit dx depuis le centre de la bulle ;
: angle sous lequel on voit dx depuis le centre de la bulle ;  : rayon de la bulle, voir la figure 1).
: rayon de la bulle, voir la figure 1).
La somme des forces 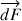 et
et 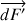 est une force
est une force 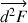 radiale, dirigée vers l’intérieur et de valeur :
radiale, dirigée vers l’intérieur et de valeur :
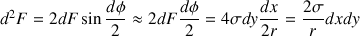 .
.
Les deux côtés 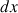 contribuent de la même façon que les côtés
contribuent de la même façon que les côtés 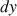 . L’élément de surface subit donc la force
. L’élément de surface subit donc la force
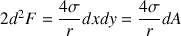
vers l’intérieur.
Cette force vers l’intérieur est compensée par la force pressante exercée par l’air emprisonné à l’intérieur de la bulle. Si l’excédent de pression de l’air intérieur à la bulle par rapport à l’air extérieur est 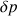 =
= 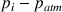 (
( 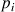 : pression à l’intérieur ;
: pression à l’intérieur ; 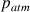 : pression atmosphérique à l’extérieur de la bulle), l’équilibre est atteint pour :
: pression atmosphérique à l’extérieur de la bulle), l’équilibre est atteint pour :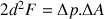 c’est-à-dire :
c’est-à-dire : 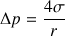
On voit ainsi que la pression 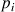 est plus grande dans une petite bulle que dans une grande.
est plus grande dans une petite bulle que dans une grande.
Lorsqu’on relie des bulles de tailles différentes, on met en communication de l’air à des pressions 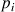 différentes. L’air de la plus petite bulle étant à une pression supérieure, il est déplacé vers la grande bulle jusqu’à ce que la plus petite bulle ait complètement disparu au profit de la plus grosse.
différentes. L’air de la plus petite bulle étant à une pression supérieure, il est déplacé vers la grande bulle jusqu’à ce que la plus petite bulle ait complètement disparu au profit de la plus grosse.
Ce qui différencie les bulles de savon des ballons de baudruche, c’est le fait que la tension superficielle dans une bulle de savon garde une valeur qui ne dépend pas de la taille de la bulle alors que la tension élastique d’une membrane de caoutchouc dépend du volume du ballon. Cette propriété apparaît lorsqu’on gonfle un ballon de baudruche : au début, il faut produire une grande pression pour arriver à le gonfler ; ensuite c’est plus facile. Lorsque le ballon est très gonflé, peu avant qu’il éclate, il faut de nouveau une grande pression pour le gonfler. La figure 2 donne l’allure qualitative de la surpression 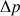 à exercer pour le gonflage en fonction du volume
à exercer pour le gonflage en fonction du volume 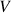 du ballon.
du ballon.
On voit sur la figure 2 que la pression intérieure peut être la même dans deux ballons de taille différente. Lorsqu’on fait communiquer l’air de deux ballons, l’ensemble évolue vers une position d’équilibre. Le cas le plus fréquent correspond à deux ballons dans la zone B de la figure 2 : c’est alors le plus petit ballon qui se vide au profit du plus grand. Si les ballons ont un volume plus petit et se trouvent tous les deux dans la zone A, ou bien s’ils sont tous les deux très gonflés et proches de l’éclatement (zone C), alors c’est le plus gros ballon qui envoie de l’air dans le plus petit.
 Remarques
RemarquesLe même raisonnement est utilisé dans l’expérience de mécanique des liquides « Faire des bulles de savon géantes »

