Un mélange d’eau, de produit vaisselle, de colle à papiers peints et de sucre est réalisé puis laissé au repos un ou deux jours. On peut alors réaliser des bulles de savon géantes, capables d’emprisonner complètement un enfant.
Fiche d’accompagnement de l’expérience:

 Matériel
Matériel- un seau ;
- du fil métallique non isolé.
- du savon de Marseille en copeaux (750 g) ;
- de la colle à papiers peints (25 g) ;
- du sucre (500 g) ;
- de l’eau (10 l) ;
- éventuellement un peu de glycérine (CH2OH–CHOH–CH2OH).
- une solution à 2,5 % de dibromostéarate de sodium (C17H33Br2COO– + Na+) dans la glycérine à 50 % (400 ml) ;
- une solution à 5 % d’alcool polyvinylique ([CH2–CHOH]n) (200 ml) ;
- de la glycérine (600 ml).
 Montage et réalisation
Montage et réalisationPour faire une solution permettant d’obtenir des bulles de savon géantes, dissoudre dans 10 l d’eau :
- 750 g de savon de Marseille en paillettes ;
- 25 g de colle à papiers peints ;
- 500 g de sucre ;
- éventuellement un peu de glycérine.
Bien remuer le mélange et le laisser reposer au moins une journée (ou encore mieux pendant trois jours). Fabriquer un anneau de 20 à 40 cm de diamètre avec du fil métallique non isolé. Plonger l’anneau dans la solution et le déplacer perpendiculairement au plan de l’anneau pour obtenir des bulles géantes (voir la figure 1).
Une autre recette de solution pour faire des bulles géantes consiste à mélanger :
- 400 ml d’une solution à 2,5 % de dibromostéarate de sodium dans une solution de glycérine à 50 % ;
- 200 ml de solution à 5 % d’alcool polyvinylique ;
- 600 ml de glycérine.
Remuer vigoureusement puis laisser reposer pendant trois jours.
Les bulles de savon réalisées avec ce deuxième mélange durent plus longtemps que les premières.
 Explications
ExplicationsLes détergents (ici le savon de Marseille et le dibromostéarate de sodium) font baisser la tension interfaciale 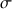 entre l’eau et l’air. Les molécules de détergent comportent la plupart du temps une partie hydrophile polaire (ici le groupement carboxylate COO–) et une partie hydrophobe apolaire (ici les longues chaînes carbonées du savon et du dibromostéarate de sodium). Les groupements hydrophiles des détergents vont au contact des molécules d’eau. La distance entre les molécules d’eau augmente. Le champ électrique diminuant en
entre l’eau et l’air. Les molécules de détergent comportent la plupart du temps une partie hydrophile polaire (ici le groupement carboxylate COO–) et une partie hydrophobe apolaire (ici les longues chaînes carbonées du savon et du dibromostéarate de sodium). Les groupements hydrophiles des détergents vont au contact des molécules d’eau. La distance entre les molécules d’eau augmente. Le champ électrique diminuant en
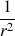
(  : distance à la charge créant le champ), les forces attractives entre molécules d’eau diminuent lorsque la distance entre ces molécules augmente. Ceci explique pourquoi la tension superficielle de l’eau diminue en présence de détergent.
: distance à la charge créant le champ), les forces attractives entre molécules d’eau diminuent lorsque la distance entre ces molécules augmente. Ceci explique pourquoi la tension superficielle de l’eau diminue en présence de détergent.
La valeur de la tension superficielle limite la hauteur à laquelle on peut tirer l’anneau hors de la solution lorsqu’on le tient verticalement. Pour faire des bulles géantes, il faut donc une solution dont la tension superficielle est faible. La justification théorique est la suivante :
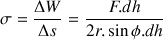
( 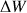 : travail nécessaire pour augmenter la surface de la bulle de
: travail nécessaire pour augmenter la surface de la bulle de 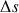 , avec
, avec 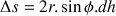 ;
;  : rayon de l’anneau de métal ;
: rayon de l’anneau de métal ; 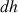 ,
, 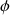 : définis sur la figure 2 ;
: définis sur la figure 2 ; 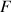 : valeur de la force nécessaire pour tirer l’anneau de
: valeur de la force nécessaire pour tirer l’anneau de 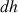 hors de la solution savonneuse).
hors de la solution savonneuse).
La tension superficielle 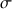 étant inversement proportionnelle à
étant inversement proportionnelle à  , avec une solution de tension superficielle plus faible on peut donc utiliser des anneaux de rayons plus grands.
, avec une solution de tension superficielle plus faible on peut donc utiliser des anneaux de rayons plus grands.
Le fil de métal doit être nu (enlever l’isolation éventuelle) pour que la solution d’eau savonneuse le mouille bien.
L’énergie de surface diminuant avec la surface, la bulle de savon tend à minimiser sa surface. La pression de l’air à l’intérieur de la bulle s’oppose à une diminution de son volume. L’existence de la bulle résulte de l’équilibre entre ces phénomènes. Examinons les calculs de façon détaillée.
Considérons un élément de surface 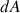 de la bulle de savon, de côtés
de la bulle de savon, de côtés 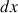 et
et 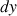 (voir la figure 3).
(voir la figure 3).
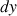 subissent de la part du reste de la bulle des forces de tension superficielle
subissent de la part du reste de la bulle des forces de tension superficielle 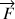 et
et 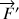 de valeur commune
de valeur commune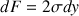 (le facteur 2 est dû au fait que la pellicule d’eau savonneuse est constituée de 2 interfaces eau-air, l’une à l’intérieur et l’autre à l’extérieur). On a :
(le facteur 2 est dû au fait que la pellicule d’eau savonneuse est constituée de 2 interfaces eau-air, l’une à l’intérieur et l’autre à l’extérieur). On a :
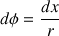
( 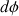 : angle sous lequel on voit dx depuis le centre de la bulle ;
: angle sous lequel on voit dx depuis le centre de la bulle ;  : rayon de la bulle, voir la figure 3).
: rayon de la bulle, voir la figure 3).
La somme des forces 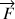 et
et 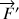 est une force
est une force 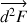 radiale, dirigée vers l’intérieur et de valeur
radiale, dirigée vers l’intérieur et de valeur
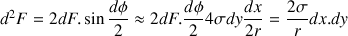 .
.
Les deux côtés 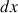 contribuent de la même façon que les côtés
contribuent de la même façon que les côtés 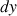 . L’élément de surface subit donc la force
. L’élément de surface subit donc la force 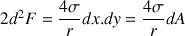 dirigée vers l’intérieur.
dirigée vers l’intérieur.
Cette force vers l’intérieur est compensée par la force pressante exercée par l’air emprisonné à l’intérieur de la bulle. Si l’excédent de pression de l’air intérieur à la bulle par rapport à l’air extérieur est 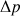 , l’équilibre est atteint pour :
, l’équilibre est atteint pour :
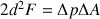 , ce qui donne
, ce qui donne 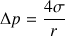 .
.
L’eau savonneuse de la bulle est entraînée vers le bas par gravité. De ce fait, l’épaisseur est très faible en certains endroits de la partie supérieure de la bulle qui peuvent céder sous l’effet de la pression intérieure : la bulle de savon éclate. Pour ralentir l’écoulement du liquide vers le bas, il faut augmenter la viscosité de la bulle. C’est pourquoi nos recettes comportent des substances destinées à augmenter la viscosité : la colle à papiers peints, le sucre, la glycérine et l’alcool polyvinylique.
L’iridescence de la bulle est due à des interférences lumineuses.
Sur la figure 4, on a représenté un rayon lumineux de lumière blanche arrivant sur la pellicule extérieure de la bulle de savon sous l’incidence 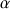 . Sur la face intérieure de la bulle, il y a ensuite réflexion de la lumière et le rayon réfracté est d’intensité plus faible qu’avant la réflexion puisqu’il y a aussi réfraction. Les rayons ainsi obtenus (rayon réfléchi du premier ordre, rayons réfractés de 3ème ordre, de 5ème ordre, etc.) sont cohérents, ils interfèrent. La différence de marche entre ces rayons dépend de l’angle d’incidence
. Sur la face intérieure de la bulle, il y a ensuite réflexion de la lumière et le rayon réfracté est d’intensité plus faible qu’avant la réflexion puisqu’il y a aussi réfraction. Les rayons ainsi obtenus (rayon réfléchi du premier ordre, rayons réfractés de 3ème ordre, de 5ème ordre, etc.) sont cohérents, ils interfèrent. La différence de marche entre ces rayons dépend de l’angle d’incidence 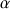 , de l’épaisseur de la couche d’eau savonneuse et de l’indice de réfraction. Il y a interférences constructives lorsque la différence de marche est égale à un multiple entier de la longueur d’onde. Un observateur regardant la bulle sous l’angle correspondant la voit de la couleur correspondant à des interférences constructives. Les différentes parties de la bulle étant vues sous des angles différents, elles apparaissent sous des couleurs différentes : on voit donc des irisations.
, de l’épaisseur de la couche d’eau savonneuse et de l’indice de réfraction. Il y a interférences constructives lorsque la différence de marche est égale à un multiple entier de la longueur d’onde. Un observateur regardant la bulle sous l’angle correspondant la voit de la couleur correspondant à des interférences constructives. Les différentes parties de la bulle étant vues sous des angles différents, elles apparaissent sous des couleurs différentes : on voit donc des irisations.
 Remarques
RemarquesVoir à ce propos la partie « Explications » de l’expérience « Forme d’une goutte d’eau ».
Le même raisonnement est utilisé dans l’expérience de mécanique des gaz « Ballons communicants ».

