Cette vidéo montre l’influence d’un aimant permanent sur le filament d’une lampe à incandescence : un curieux mouvement d’oscillation dû à l’attraction puis la répulsion entre l’aimant et le filament parcouru par le courant périodique fourni par le secteur, ce qui le transforme en un aimant de polarité variable.
Fiche d’accompagnement de l’expérience:

 Matériel
Matériel-
une lampe à incandescence transparente ;
-
un aimant droit ;
-
une douille de lampe munie d’un fil de branchement sur le secteur ;
-
des lunettes de soleil ou un filtre coloré.
 Montage et réalisation
Montage et réalisationUne lampe à filament de carbone est traversée par un courant secteur alternatif (50 Hertz).
Le filament de cette lampe, porté à incandescence, est constitué de plusieurs spires tenues à leurs extrémités par les 2 conducteurs reliés au culot de la lampe et en leur centre par un support inerte qui empêche l’ensemble de prendre une trop grande amplitude de déplacement.
Approchons un aimant permanent du filament: nous observons que les premières spires sont floues. (les suivantes restent immobiles à cause du support fixe qui maintient immobile la spire centrale)
En effet les spires sont soumises successivement à des forces de sens opposés à chaque alternance du courant, qui les font se déplacer alternativement de gauche à droite et vice versa.
Plus l’aimant permanent est proche des spires, plus celles-ci voient leur mouvement prendre de l’amplitude et diminuer lorsqu’on écarte l’aimant.
 Explications
ExplicationsLe courant qui circule dans le filament oscille à la fréquence f = 50 Hz qui est celle du secteur. Le filament se trouve dans le champ magnétique créé par l’aimant .
Les spires parcourues par un courant se comportent comme des aimants munis d’une face nord et d’une face sud. Lorsque le courant s’inverse, les pôles nord et sud s’inversent et les spires sont alternativement attirées ou repoussées par l’aimant permanent.
Si l’on veut avancer dans la compréhension du phénomène, l’énoncé de cette propriété s’appuie sur le calcul de la force qui s’exerce sur les spires .
Un conducteur électrique élémentaire de longueur très petite 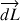 traversé par un courant I et placé dans un champ magnétique
traversé par un courant I et placé dans un champ magnétique 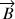 subit la force de Laplace élémentaire
subit la force de Laplace élémentaire 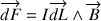
L’intensité de la force 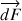 est proportionnelle à l’amplitude du champ magnétique et du courant. Elle est donc plus forte quand on approche l’aimant.
est proportionnelle à l’amplitude du champ magnétique et du courant. Elle est donc plus forte quand on approche l’aimant.
Elle est perpendiculaire au plan contenant le conducteur élémentaire et le champ magnétique.
Son sens est tel que le trièdre formé par le sens du courant, le champ magnétique et la force forment un trièdre direct. Elle change donc de sens quand le courant s’inverse.
Les spires peuvent être considérées comme composées d’une suite de tels petits tronçons élémentaires .
Lorsqu’on additionne vectoriellement toutes les forces élémentaires agissant sur chaque « tronçon », on obtient une force résultante s’exerçant sur la spire suivant l’axe de la spire . Cette force résultante est proportionnelle à B, elle est donc plus intense quand on approche l’aimant. Elle change de sens quand le sens du courant s’inverse.
Cette force doit son nom au physicien français Pierre Simon de Laplace (1749-1827).
 Remarques
RemarquesPour bien observer le phénomène il est préférable de regarder la lampe à travers des lunettes de soleil ou à travers des filtres colorés (éventuellement plusieurs filtres superposés) car sans protection on serait ébloui par la lumière vive et on ne verrait pas les oscillations.
 Références
RéférencesUniversité du Mans : physique et simulations numériques

