• une boîte de conserve cylindrique vide (diamètre : au moins 10 cm)

• un petit objet pour créer une surcharge (au moins 75 g), par exemple des pièces de monnaie ou un aimant

• un plan incliné, par exemple un classeur

• accessoire : du ruban adhésif

Coller avec du ruban adhésif une surcharge sur la paroi intérieure de la boîte de conserve. Placer alors la boîte dans la position 1 sur le plan incliné (voir figure ci_dessous).

Le point A sur la figure représente la génératrice du cylindre en contact avec le plan incliné et le point G le centre d’inertie de la boîte.

La boîte lâchée dans la position 1 remonte la pente jusqu’à la position 2 (voir figure).

Pour rendre l’expérience plus étonnante il faut cacher l’intérieur de la boîte à la vue des spectateurs en ne leur montrant que le fond de la boîte ou en fermant le côté ouvert par un couvercle. On peut poser la boîte au départ près du sommet du plan incliné et s’arranger pour qu’elle passe de l’autre côté : dans ce cas il n’est pas nécessaire de prévenir les spectateurs qu’elle ne peut pas monter indéfiniment.

Il est important de bien choisir la valeur de l’inclinaison du plan incliné. Si l’inclinaison est trop forte, la boîte peut patiner ou bien descendre la pente mais si elle est inférieure à 4°, l’expérience réussit sans problème. Avec une inclinaison supérieure à 4°, il peut être nécessaire de placer deux élastiques autour de la paroi latérale symétriquement par rapport aux bords afin d’améliorer l’adhérence de la boîte sur le plan incliné. Avec une boîte de conserve courante (diamètre d’environ 10 cm), si la surcharge a une masse d’au moins 75 g on peut incliner le plan jusqu’à 10°. C’est sensiblement l’inclinaison d’un classeur contenant quelques feuilles et reposant sur un plan horizontal.

La distance maximale parcourue par la boîte est une demi circonférence, on a donc intérêt à prendre une boîte de grand diamètre. Les boîtes plus grandes étant plus lourdes, il faudra vraisemblablement coller une surcharge plus lourde.

Les aimants font des surcharges pratiques à utiliser car ils n’ont pas à être collés et on peut les enlever discrètement quand un spectateur demande à inspecter l’intérieur de la boîte.

Le centre de gravité, initialement sur l’axe de symétrie du cylindre, se trouve déplacé par l’ajout de la surcharge. Supposons pour simplifier que le nouveau centre de gravité G se trouve à l’endroit de la surcharge (voir figure ).
Dans la position 1, le poids 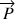qui s’applique en G a un moment 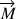par rapport à la génératrice du cylindre en contact avec le support. Ce moment entraîne un mouvement de rotation vers le haut. Sa valeur est :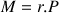

(r : distance de la droite d’action D du poids à l’axe de rotation passant par A).

Après être remontée le long du plan incliné, la boîte atteint la position 2 dans laquelle la droite d’action du poids passe par A. On a alors r = 0 et donc M = 0 : c’est une position d’équilibre.

Un léger déplacement de la boîte dans un sens ou dans l’autre à partir de la position 2 la ramène dans la même position : c’est une position d’équilibre stable.

Pour expliquer le principe de l’expérience nous avons fait l’hypothèse simplificatrice que le centre de gravité G de la boîte se trouvait sur la paroi. Il reste à préciser à quelle distance de A doit se trouver la droite D pour que la boîte puisse effectivement monter.

Le moment du poids fera remonter la boîte si la droite d’action du poids (D) rencontre le plan incliné au dessus de A.

Il faut que, sur la figure , la droite D se trouve à gauche de la droite , verticale passant par A. Le point G doit donc être dans la zone grisée à gauche de la droite .

Le rayon de la boîte étant R, la distance minimale entre G et le centre de la boîte permettant de remonter est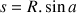
.
Pour s et R donnés, il faut donc que l’inclinaison soit telle que
.
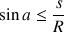