Les forces de frottement sont en général un inconvénient que l’on cherche à minimiser. Mais dans cette expérience, lorsqu’elles se conjuguent avec la précession d’une toupie, elles donnent lieu à un comportement inattendu : la toupie bascule et se met à tourner en équilibre sur sa tige ! Etonnant, non ?


 Fiche d’accompagnement de l’expérience:

• une toupie en plastique ou en bois

• une soucoupe ou une assiette

Tenir la toupie par la tige et la faire tourner : le point de contact de la toupie avec le support décrit une spirale qui s’écarte du point de contact initial.
Au cours de son mouvement, la toupie s’incline de plus en plus.
Lorsque la pointe de la tige de la toupie touche le support, la toupie se redresse brusquement sur sa tige et continue à tourner dans cette position.

La toupie tourne « normalement » sans basculer sur sa tige si on la pose sur la table de telle sorte que son moment cinétique soit parallèle à son axe de symétrie, on a représenté sur les figures suivantes la projection sur la table de l’axe de symétrie de la toupie).

Si le moment cinétique n’est pas parallèle à l’axe de symétrie, on peut le décomposer suivant la direction de l’axe de symétrie et suivant une direction perpendiculaire et écrire

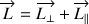
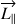(  : composante du moment cinétique parallèle à l’axe de symétrie de la toupie ;
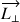 : composante perpendiculaire à l’axe de symétrie).
L’axe de précession de la toupie est parallèle à 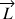 mais il passe par le centre d’inertie G de la toupie et non pas par le point de contact A de la toupie avec la table.

La force de frottement 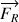 exercée par la table sur la toupie peut être décomposée en force de frottement de glissement et force de frottement de roulement.

Elle a pour moment  .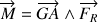
On a :
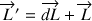 (1)
et
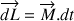 (2)
(dt : durée pendant laquelle le moment 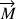 agit sur la toupie ;  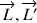: moment cinétique de la toupie).
Comme la composante de 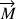 sur l’axe de symétrie de la toupie est de sens opposé à  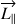, il résulte des relations précédentes que la valeur de  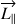diminue.
Simultanément, la valeur de 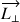 augmente car la composante de  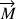perpendiculaire à l’axe de symétrie est de même sens que  .
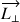Résumons : les frottements entraînent une diminution du moment cinétique 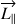 parallèle à l’axe de symétrie de la toupie et une augmentation du moment cinétique  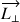perpendiculaire à cet axe.

Si l’axe de symétrie de la toupie est horizontal, alors 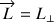 et  .
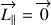Le moment 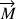 provoque une augmentation de la valeur de  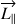car 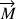 possède une composante suivant l’axe de symétrie de la toupie qui n’est pas nulle et qui est de même sens que 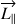Simultanément, la valeur de  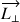diminue car la composante de  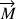perpendiculaire à l’axe de symétrie est de sens contraire à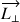 
Les relations (1) et (2) montrent que lorsque la tige de bois est inclinée vers le bas, la valeur de 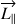 augmente car la composante de  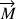parallèle à l’axe de symétrie est de même sens que  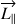.Simultanément, la valeur de  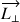diminue car la composante de  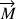perpendiculaire à l’axe de symétrie et  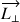sont de sens contraires.

Lorsque la tige de la toupie touche la table en B, elle est soumise à une force de frottement 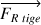 dont le moment est  .
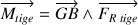La toupie, de moment cinétique 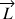 , est soumise au moment global  .
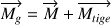On a :
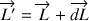 (1)
et
 (3)
(dt : durée d’action du moment global 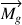 ; , : moment cinétique de la toupie).
Il en résulte que la valeur de 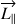 augmente car la composante de  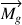parallèle à l’axe de symétrie est de même sens que  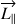, tandis que la valeur de 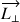diminue car la composante de  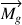perpendiculaire à l’axe et  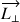sont de sens contraires.
Lorsque la toupie est renversée et son axe de symétrie vertical, on a 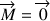 car le seul contact entre la toupie et la table se situe au bout de la tige.
Comme on ne peut pas définir de direction pour les forces de frottement, il n’y a plus de moment global 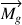 susceptible de modifier  .
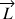La toupie continue donc à tourner verticalement en position renversée. Des perturbations dues à des irrégularités de la surface de la table peuvent entraîner une inclinaison de l’axe de symétrie de la toupie, mais le moment 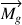 qui en résulte ramène la toupie dans sa position verticale renversée qui est donc une position d’équilibre stable.
Essayons de décrire, en termes plus simples sans équations mathématiques, le comportement de la toupie tippe top.

Lorsqu’on met en rotation la toupie, le fait que le centre de masse soit en dessous du centre de la sphère, induit un déplacement de ce centre par rapport à l’axe de rotation qui reste perpendiculaire à la surface sur laquelle la toupie est en rotation.
La composante du moment angulaire le long de l’axe reste prépondérante avant et après inversion , bien qu’au regard de la toupie, le sens de rotation ait été inversé .
Au cours du retournement le centre de masse de la toupie est plus haut que précédemment ;son énergie cinétique de rotation diminue , fournissant suffisamment d’énergie potentielle pour élever le centre de masse . Ainsi, la vitesse angulaire totale et le moment cinétique total diminuent au cours du processus d’inversion .
Ce processus nécessite l’action d’un couple , mais ce couple ne peut être fourni par gravité ou par les forces normales exercées au niveau du point de contact avec la surface sur laquelle repose la toupie.
L’explication réside dans la présence de forces de frottement de glissement entre le fond arrondi de la toupie et la surface sur laquelle elle est en train de tourner .
Ces forces résultent du déplacement centrifuge du centre de masse lorsque la toupie est mise en rotation.
Si la vitesse de rotation initiale, communiquée au début à la toupie lorsqu’elle est mise en rotation, est suffisamment élevée , la précession et les oscillations du haut de la toupie peuvent éventuellement entraîner, lorsque le bord de la tige entre en contact avec la surface sur laquelle est posée la toupie,un mouvement de rotation de celle-ci en position inversée .

Dans les explications, nous avons négligé les phénomènes suivants : la toupie « s’enfonce » un peu dans le support (le contact n’est donc pas parfaitement ponctuel) et elle possède une certaine élasticité. Dans les expériences que nous avons réalisées, la toupie a parfois décollé de la table et effectué de véritables sauts. Pour en rendre compte de façon théorique, il faudrait supposer que la toupie repose sur un ressort. Ce ressort théorique compliquerait exagérément la description du mouvement de la toupie, c’est pourquoi nous ne l’avons pas pris en considération.

La toupie renversable (tippy top en anglais) est un jouet ancien pour lequel Helene Sperl de Munich a déposé un brevet en 1891. Les explications qui figurent dans la description de son brevet sont complètement erronées. Les premières explications présentant des équations correctes datent seulement des années 1950.
Wolfgang Pauli et Niels Bohr fascinés par une toupie renversable.

On reprend ici l’expérience de la toupie renversable, mais ici la toupie est réalisée avec quatre billes de verre collées pour former un tétraèdre. C’est plus facile à trouver, et ça marche aussi bien !

une explication plus succincte :
La toupie Tippe Top ou « Pourquoi la toupie tippe top se retourbe-t-elle? »
pour les matheux :
La toupie Tippe-Top