Une lentille à bords minces, convergente lorsqu’elle se trouve dans l’air, peut devenir divergente lorsqu’elle est plongée dans l’eau. Les propriétés d’une lentille ne dépendent donc pas uniquement de sa forme, il faut aussi tenir compte du milieu dans lequel elle se trouve.
Fiche d’accompagnement de l’expérience:
 Matériel
Matériel-
2 verres de montre identiques
-
un aquarium rempli d’eau
 Montage et réalisation
Montage et réalisationPlacer les deux verres de montre bord à bord pour former une lentille biconvexe. Veiller à bien ajuster les bords de façon à obtenir une bonne étanchéité entre l’intérieur et l’extérieur grâce à de la pâte à modeler.
Lorsque les deux verres de montre sont immergés dans l’eau, ils constituent une lentille d’air dans l’eau, il s’agit d’une lentille biconvexe.
Le faisceau translaté parallèlement à l’axe de la lentille s’écarte de cet axe : la lentille est divergente.
Réaliser la même expérience mais en remplissant d’eau la cavité entre les deux verres de montre puis en les sortant de l’eau. On a ainsi une lentille d’eau entourée d’air.
Le faisceau translaté parallèlement à l’axe de la lentille se rapproche de cet axe : la lentille est convergente.
 Explications
ExplicationsDans l’expérience ci-dessus, les deux verres de montre forment l’enveloppe extérieure d’une lentille biconvexe.
Dans le premier cas, il s’agit d’une lentille d’air plongée dans l’eau, dans le deuxième cas, d’une lentille d’eau plongée dans l’air. Dans un premier temps, on ne tiendra pas compte du verre dont sont constitués les verres de montre.
Il faut examiner dans chacun des cas si l’on réalise une lentille divergente ou une lentille convergente. Par suite du phénomène de réfraction, un rayon incident parallèle à l’axe optique se rapproche de l’axe après la traversée d’une lentille convergente, et s’en éloigne après la traversée d’une lentille divergente.
On peut considérer une lentille comme un assemblage de prismes élémentaires.
Pour déterminer le caractère convergent ou divergent de la lentille, il suffit donc de déterminer si un rayon qui arrive perpendiculairement au plan de symétrie du prisme se trouve dévié dans la direction opposée à l’arête du prisme ou au contraire vers l’arête. Si ce rayon est dévié en s’éloignant de l’arête, on a une lentille convergente, et dans le cas contraire une lentille divergente.
La déviation angulaire totale 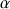 que subit un rayon qui arrive sur l’une des faces du prisme est:
que subit un rayon qui arrive sur l’une des faces du prisme est:
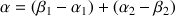
(les angles sont comptés positivement dans le sens trigonométrique et négativement dans le sens des aiguilles d’une montre).
L’indice de réfraction de l’eau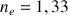
est supérieur à celui de l’air 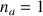 .
.
Un rayon qui passe de l’air à l’eau est donc réfracté en se rapprochant de la normale au dioptre au point d’incidence et il s’en éloigne lors du passage de l’eau à l’air.
Il faut donc distinguer les cas suivants pour le calcul de 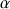 :
:
1. Prisme d’eau plongé dans l’air:
D’après les explications précédentes on a alors :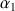 et
et 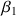 positifs,
positifs,
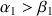
et
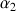 et
et 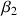 négatifs,
négatifs,
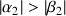
donc
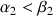
En reportant cette relation dans
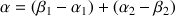 ,
,
on obtient un angle 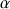 négatif. Le rayon émergent s’éloigne de l’arête du prisme. Une lentille d’eau biconvexe plongée dans l’air est donc une lentille convergente.
négatif. Le rayon émergent s’éloigne de l’arête du prisme. Une lentille d’eau biconvexe plongée dans l’air est donc une lentille convergente.
2. Prisme d’air plongé dans l’eau:
D’après les explications précédentes on a alors :
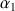 et
et 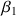 positifs,
positifs,
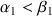
et
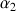 et
et 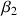 négatifs,
négatifs,
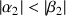
donc
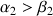
En reportant cette relation dans
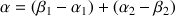 ,
,
on obtient un angle 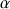 positif. Le rayon émergent se rapproche de l’arête du prisme. Une lentille d’air biconvexe plongée dans l’eau est donc une lentille divergente.
positif. Le rayon émergent se rapproche de l’arête du prisme. Une lentille d’air biconvexe plongée dans l’eau est donc une lentille divergente.
Il reste à justifier pourquoi on peut négliger la traversée du verre dont sont constitués les verres de montre. Jusqu’ici, on n’a tenu compte que des angles sous lesquels les rayons entrent dans le prisme ou en sortent. Montrons donc que la traversée du verre ne modifie pas ces angles.
Sur la figure ci-contre, on a représenté un rayon lumineux qui traverse les milieux 1, 2 et 3 séparés par des surfaces planes parallèles. Les angles entre ce rayon et les normales aux points d’incidence vérifient les relations suivantes: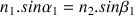
et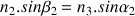
( 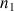 ,
, 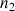 et
et 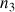 : indices de réfraction des milieux 1,2 et 3).
: indices de réfraction des milieux 1,2 et 3).
Comme les deux surfaces de séparation sont parallèles, on a:
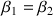 .
.
On en déduit alors :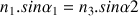
Cette relation correspond au passage direct, sans milieu 2, du milieu 1 (angle d’incidence 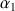 ) au milieu 3 (angle de réfraction
) au milieu 3 (angle de réfraction 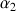 ) .
) .
Le verre correspond au milieu 2, donc la traversée du verre peut être négligée.
 Remarques
RemarquesDes gouttes d’eau sur une feuille de plastique transparente ont une surface extérieure légèrement incurvée : ce sont donc des lentilles d’eau plan-convexes. Comme elles sont entourées d’air elles se comportent comme des lentilles convergentes. Des bulles d’air dans l’eau se comportent en revanche comme des lentilles divergentes.
 Références
RéférencesUniversité en Ligne: lentilles épaisses ; lentilles minces

