Fixez sur une glace plane une feuille de plastique transparent, placez-vous à une distance quelconque de cette glace et dessinez sur la feuille les contours de votre visage, tel que vous le voyez à travers le miroir. Pourquoi ce dessin est-il toujours deux fois plus petit que votre visage, quelle que soit la distance à laquelle vous vous êtes placé ? Le titre du clip vous le dit, c’est un paradoxe…
En dessinant son visage sur un miroir, on détermine quelle est la taille minimale du miroir permettant de voir son visage en entier.
Fiche d’accompagnement de l’expérience:
Matériel-
un miroir de largeur au moins égale à la moitié de la largeur du visage et de hauteur au moins égale à la moitié de la hauteur du visage
-
un transparent pour rétroprojecteur et un stylo pour transparents ou une craie grasse
-
accessoires : du ruban adhésif, du détergent liquide pour la vaisselle
Montage et réalisationL’expérimentateur doit se placer devant le miroir de façon à y voir entièrement son visage.
Fixer un transparent sur le miroir avec du ruban adhésif.
L’expérimentateur dessine alors les traits de son visage sur le transparent.
Fixer ensuite le dessin obtenu sur une vitre transparente derrière laquelle l’expérimentateur place son visage.
Constater que le dessin obtenu a une taille moitié de celle du visage.
La taille du dessin reste constante lorsque l’expérimentateur fait varier sa distance au miroir en déplaçant son œil sur une droite perpendiculaire au miroir
On peut faire le dessin à la craie grasse directement sur le miroir si l’on n’a ni transparent ni feutre spécial. Cette méthode présente cependant un inconvénient car on ne peut pas détacher le dessin du miroir pour comparer sa taille avec celle de l’objet. On peut ensuite nettoyer les traces de craie grasse qui restent sur le miroir avec un peu de liquide vaisselle.
ExplicationsLa figure suivante permet d’expliquer les faits expérimentaux :
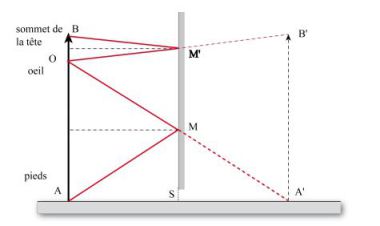
Pour que la personne puisse se voir en entier par réflexion sur le miroir il faut qu’un rayon, issu du sommet de sa tête B, passe après réflexion sur le miroir par son oeil O. De même un rayon issu de ses pieds A doit également après réflexion sur le miroir passer par son oeil.
Ce qui conduit à la figure ci-dessus où les rayons BM’O et AMO et ont été tracés en tenant compte des lois de la réflexion.
Nous voyons donc qu’il est possible de limiter la hauteur du miroir à la distance MM’ puisque la partie extérieur à MM’ n’interviendra pas dans le cheminement des rayons réfléchis.
Calculons MM’: M est situé sur la médiatrice de OA donc :
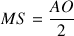
de même M’ est situé sur la médiatrice de OB donc :
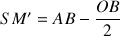
ce qui nous permet de déduire :
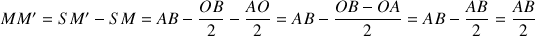
Nous n’avons pas eu besoin de préciser la position du miroir par rapport à la personne pour conduire le raisonnement précédent. La valeur de MM’ trouvée est indépendante de la position du miroir par rapport à l’observateur.
RemarquesLes explications précédentes correspondent au cas où les yeux se trouveraient dans le plan qui passe par A et B et qui est perpendiculaire à la figure .
En réalité, les yeux sont un peu plus éloignés du miroir que le segment AB. A’B’ est donc un peu supérieur à AB. L’écart entre les longueurs A’B’ et AB est plus faible si l’on impose une distance entre le visge et le miroir plus grande.
Nous conseillons donc de ne pas faire réaliser l’expérience par des enfants car ils n’ont pas les bras assez longs.
RéférencesUniversité en Ligne :miroir plan