• de la ficelle (longueur : environ 1 m)

• deux masses égales (100 à 200 g)

• des supports de laboratoire (tiges et noix)

Fabriquer deux pendules simples identiques, avec deux ficelles de même longueur auxquelles on a accroché deux masses égales.

En les écartant de la verticale et en les faisant osciller, on constate bien que les pendules sont synchrones, et aussi qu’ils s’immobilisent à la même hauteur.

Recommencer l’expérience en intercalant sur le trajet d’un des pendules une tige métallique qui va raccourcir sa longueur pendant un instant égal à une demie période.

Observer attentivement le mouvement des deux pendules : cette fois, ils ne sont plus synchrones, car à chaque oscillation le pendule dont la longueur a été raccourcie gagne du temps sur le second.

Mais les deux pendules s’immobilisent à la même hauteur, aussi bien à gauche qu’à droite de leur support.

Ceci est une conséquence directe de la conservation de l’énergie mécanique, que cette expérience très simple permet de mettre en évidence.

Le pendule de Galilée est un pendule simple dont la longueur varie au cours du temps.

Les deux demi-oscillations correspondent à des longueurs différentes. La période d’un pendule simple de longueur l et de faible amplitude est donnée par la formule :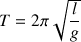
}
(l : longueur du fil ; g : valeur de l’accélération de la pesanteur).

La période de la demi-oscillation correspondant à la longueur la plus faible est donc inférieure à celle de l’autre demi-oscillation. Il en résulte que les oscillations du pendule ne présentent pas de symétrie dans l’espace ni dans le temps, donc que le pendule est anharmonique.

Le centre de gravité de la masse qui oscille atteint cependant la même hauteur à ses deux points de rebroussement car en ces deux points l’énergie potentielle est égale à l’énergie totale qui reste constante au cours du mouvement si l’on néglige les frottements.