Une bouteille en plastique percée de plusieurs trous montre que la pression dans un liquide augmente avec la profondeur d’immersion. Cette expérience facile à réaliser est une vérification du principe de Torricelli.
Fiche d’accompagnement de l’expérience:
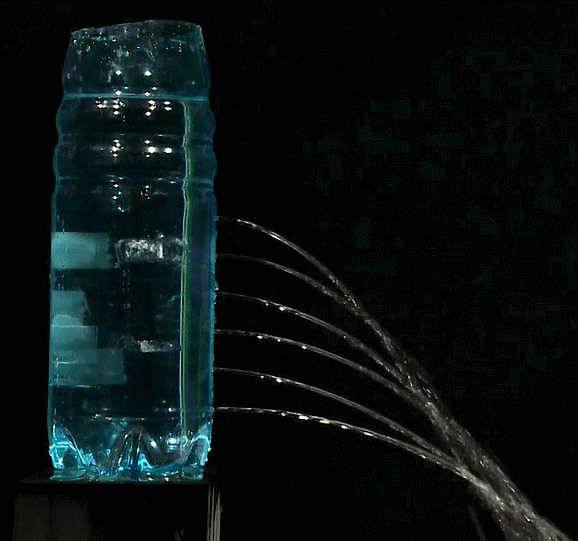
 Matériel
Matériel-
une boîte à café en métal ou une boîte de conserve ou une boîte en plastique de grande taille ou une bouteille en plastique ;
-
du ruban adhésif ;
-
un mètre à mesurer ;
-
éventuellement un tuyau de caoutchouc pour amener l’eau ;
-
accessoires : un marteau, un clou, un bec Bunsen et une pince.
 Montage et réalisation
Montage et réalisationFaire plusieurs trous (six ici) dans la paroi latérale d’une boîte de conserve (ou d’une boîte en plastique ou d’une bouteille en plastique) à l’aide d’un clou et d’un marteau.
Avec un récipient en plastique, on peut également faire chauffer le clou dans la flamme d’un bec Bunsen et l’appliquer ensuite sur la paroi pour faire fondre le plastique.
Les trous doivent se trouver sur une même verticale mais à des hauteurs différentes.
Le premier trou doit être percé à la moitié du niveau maximal de l’eau dans le récipient, les autres doivent être situés à la même distance du trou central mais de part et d’autre de celui-ci.
Boucher les trous avec un même morceau de ruban adhésif puis remplir le récipient avec de l’eau.
Enlever rapidement le ruban adhésif : l’eau sort par tous les trous en suivant des trajectoires paraboliques.
Plus un trou est bas, plus le rayon de courbure à l’origine de la parabole correspondante est grand donc plus la parabole est « plate » localement.
Les paraboles sont de moins en moins plates lorsque le niveau d’eau dans le récipient diminue. Pour pouvoir comparer sérieusement les paraboles (par exemple les photographier et faire des mesures sur les photos), il faut prévoir de garder constant le niveau dans le récipient en installant un tuyau d’arrivée d’eau.
 Explications
ExplicationsUn théorème, énoncé en 1646 par Evangelista Torricelli (1608-1647), dit que la vitesse 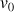 d’un fluide parfait s’écoulant par un trou situé à la profondeur h sous le niveau du liquide contenu dans le récipient est égale à la vitesse atteinte par un objet tombant en chute libre sur la même hauteur h. On en déduit la relation suivante :
d’un fluide parfait s’écoulant par un trou situé à la profondeur h sous le niveau du liquide contenu dans le récipient est égale à la vitesse atteinte par un objet tombant en chute libre sur la même hauteur h. On en déduit la relation suivante :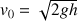 (1)
(1)
(g : intensité de la pesanteur).
Cette relation peut également être déduite de la loi de Bernoulli.
La surpression Δp à la profondeur h dans un liquide de masse volumique ρ vaut :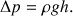
En remplaçant h dans la relation (1), on obtient :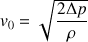
La vitesse initiale 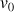 du liquide s’écoulant par le trou est donc liée à la pression du liquide dans le récipient à cet endroit. Plus
du liquide s’écoulant par le trou est donc liée à la pression du liquide dans le récipient à cet endroit. Plus 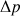 est grande, plus
est grande, plus 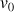 est grande, donc plus le rayon de courbure de la parabole à cet endroit est grand (c’est-à-dire plus la parabole est « plate » localement). Autrement dit, plus le trou est bas, plus la parabole est plate et car plus la pression est grande.
est grande, donc plus le rayon de courbure de la parabole à cet endroit est grand (c’est-à-dire plus la parabole est « plate » localement). Autrement dit, plus le trou est bas, plus la parabole est plate et car plus la pression est grande.
 Remarques
RemarquesLa position du récipient peut gêner l’interprétation. Si le récipient est posé directement sur le sol, on voit les jets d’eau arriver sur le sol à la hauteur du fond du récipient : c’est alors le jet issu du trou du milieu qui a parcouru la plus grande distance horizontale et non pas le jet possédant la plus grande vitesse initiale, c’est-à-dire le jet du dessous. Intuitivement, on s’attend à ce que la portée du jet augmente avec la profondeur du trou si bien que la plupart des livres présentent pour cette expérience des schémas qualitatifs faux. De quoi s’agit-il exactement ?
Considérons une goutte d’eau qui quitte le trou situé à la hauteur h sous la surface de l’eau avec la vitesse horizontale
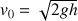 .
.
La distance horizontale x parcourue par la goutte pendant le temps t avant de toucher le sol est :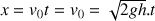 .
.
Pendant ce temps, la goutte tombe également de y = H – h, en appelant H est la hauteur de l’eau du récipient au-dessus du sol. On a alors :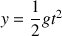 ,
,
soit
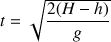
La relation entre la portée x du jet et la profondeur h du trou est donc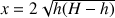
Cherchons pour quelle valeur de h la portée x est maximale, c’est-à-dire pour quelle valeur de h la dérivée de x par rapport à h s’annule. On trouve que c’est pour h = H/2. La portée maximale est alors x = H. Comme on le voit en examinant les valeurs de la fonction x pour h = H/2 + ε et h = H/2 – ε, x(h) est symétrique par rapport à la valeur h = H/2. Finalement, on a montré que lorsque le sol est à la même hauteur que le fond du récipient, c’est le jet issu du trou central situé à la profondeur h = H/2 qui a la portée la plus longue et que les jets issus de deux trous symétriques par rapport au trou central ont des portées égales. Pour vérifier ces résultats, il faut bien percer les trous aux endroits indiqués.
Le calcul précédent a été fait en négligeant les frottements. Ces résultats restent cependant valables d’un point de vue qualitatif et permettent de mettre en défaut les illustrations de certains ouvrages. Pour contrôler rapidement si les illustrations sont correctes on peut faire les deux vérifications suivantes :
-
Le récipient étant posé sur le sol, son niveau d’eau à la hauteur H au-dessus du sol, le jet d’eau issu du trou à la profondeur H/2 a-t-il une portée H sur le sol ?
-
Deux jets d’eau issus de trous symétriques par rapport au trou central ont-ils la même portée ?
On peut éviter cette situation paradoxale en surélevant la boîte de quelques dizaines de centimètres par rapport au sol. En choisissant bien la hauteur h* du fond de la boîte par rapport au sol, on voit les jets arriver sur le sol dans le « bon ordre », c’est-à-dire dans l’ordre de la profondeur des trous. Si cela vous amuse, vous pouvez calculer la valeur minimale de h* pour que des jets issus des profondeurs 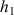 ,
, 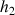 , …,
, …, 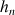 connues arrivent au sol « dans l’ordre ». Quelle est l’équation de l’enveloppe de toutes les paraboles pour un niveau d’eau H donné ?
connues arrivent au sol « dans l’ordre ». Quelle est l’équation de l’enveloppe de toutes les paraboles pour un niveau d’eau H donné ?
En ramenant par la pensée en un même point les sommets de toutes les paraboles, on verrait les jets d’eau arriver « dans l’ordre » sur le sol, puisque les paraboles s’aplatissent lorsque le trou est plus bas.
Les expériences « Prévoir où sortent les bulles » et « Comment remplir une boîte de lait concentré » se rapportent au même thème.

