• Lorsque l’air contenu dans un tuyau est mis en vibration, il peut produire des sons ; c’est sur ce principe que repose la production des sons dans les instruments à vent, que ce soient les bois, les cuivres, la cornemuse ou l’orgue. Pour cela, il est nécessaire d’entretenir dans le tuyau une circulation d’air soumise à une perturbation périodique.
• Dans l’expérience décrite ici, la circulation d’air est assurée par la rotation du tuyau : l’air situé à l’extérieur de l’extrémité libre du tuyau a une vitesse v par rapport à l’air contenu dans le tuyau et la valeur de v dépend de la vitesse de rotation du tuyau. L’air situé à l’extérieur du tuyau est donc à une pression plus basse que l’air situé dans le tuyau. Lorsque le tuyau a un mouvement de rotation constant, il est donc parcouru par un courant d’air entrant par l’extrémité tenue à la main et sortant par l’extrémité libre. La perturbation du courant d’air est produite par les cannelures du tuyau ou par son bord : il apparaît des turbulences et l’écoulement de l’air n’est donc pas laminaire. C’est ainsi que naissent des oscillations de pression dans le tuyau qui sont constituées par la superposition de toutes sortes de fréquences.
  Certaines de ces fréquences sont renforcées parce qu’elles correspondent aux fréquences propres d’une colonne d’air de longueur L. On a alors :
  

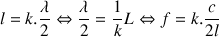
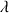  ( : longueur d’onde ; c : célérité du son ; k = 1, 2, … : nombre entier).

• Le tuyau étant ouvert aux deux extrémités, il y a des ventres de vibration aux deux extrémités (voir la figure).
• D’après cette relation, on devrait pouvoir produire une infinité de sons : un fondamental ou harmonique de rang 1 pour k = 1 et des harmoniques pour k = 1, 2, … En fait, on ne réussit à produire que certains des sons prévus par le calcul : en général, le fondamental et les quatre premiers harmoniques. L’expérience montre que l’ordre k de l’harmonique émis par le tuyau dépend de la vitesse relative v de l’air et donc de la vitesse de rotation du tuyau (celle-ci n’est finalement limitée que par les possibilités physiques de l’expérimentateur qui fait tourner le tuyau). Lorsque la vitesse de rotation du tuyau est faible, on ne peut produire que des sons de basse fréquence car les fluctuations de pression qui donnent naissance au son sont produites par l’écoulement de l’air sur les cannelures. Plus le tuyau tourne vite, plus la vitesse d’écoulement de l’air dans le tuyau est élevée et plus les fluctuations de pression sont rapprochées.
• • En prenant
    
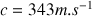
    pour la célérité du son dans l’air à 20°C et un tuyau de longueur L = 1 m, les sons qu’on peut obtenir sont les suivants :
    • le fondamental à 171 Hz
      ( ),
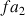    • l’harmonique de rang 2 (une octave au-dessus du fondamental) à 342 Hz
      ( ),
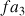    • l’harmonique de rang 3 (une quinte au-dessus de l’harmonique de rang 2) à 513 Hz
      ( ),
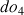    • l’harmonique de rang 4 (une quarte au-dessus de l’harmonique de rang 3) à 684 Hz
      ( ),
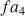    • l’harmonique de rang 5 (une tierce majeure au-dessus de l’harmonique de rang 4) à 855 Hz
      ( ),
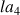    • et éventuellement encore l’harmonique de rang 6 (une tierce mineure au dessus de l’harmonique de rang 5) à 1026 Hz
      ( )

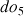    en indiquant entre parenthèses les notes les plus proches si l’on prend comme référence le la du diapason international
    (440 Hz = ).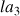
    Jusqu’à l’harmonique de rang 4, les sons émis par un tuyau de 1 m correspondent au registre d’une voix d’alto.

Quelques points de repère pour comparer les sons produits par un tuyau de 1 m avec les registres des chanteurs : pour une voix de basse, le

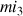
est déjà aigu et le fameux « contre-ut » des ténors est le
.
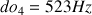De même, le

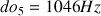
(contre-ut des voix de femmes) est aigu pour une voix de soprano mais les voix des soprano-colorature doivent monter encore plus haut, en particulier dans de nombreux opéras de bel-canto et aussi dans des opéras français d’Adam Meyerbeer ; Thomas Giuseppe Verdi (1813‑1901) a introduit dans son opéra « I due Foscari » une aria comportant un contre mi-bémol à destination du ténor Giovanni Mario (1810‑1883).

La soprano allemande Erna Sack (1898‑1972) peut être considérée comme une voix exceptionnelle qui réussissait à chanter des notes au-dessus du
.
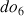Richard Strauss a modifié certaines parties de son opéra « La femme silencieuse » pour tenir compte de ses dons particuliers. Il faut absolument écouter des enregistrements d’Erna Sack (maintenant disponibles en CD) : on ne peut pas imaginer qu’une voix humaine puisse produire de tels sons tant qu’on ne l’a pas entendu de ses propres oreilles !