• 2 feuilles de papier identiques (taille A4)

• du ruban adhésif

• accessoires : un compas et des ciseaux

Découper dans du papier deux disques de rayon 8 cm.

Tracer un angle au centre de 60° dans le premier, de 180° dans le deuxième et découper le disque le long d’un des rayons correspondants jusqu’au centre.

Superposer le rayon qui a été découpé et le deuxième rayon du secteur angulaire et coller par un peu de ruban adhésif : on a ainsi fabriqué deux cônes (voir la figure ).

Le cône le plus étroit est celui qui correspond à l’angle au centre le plus grand, mais les deux cônes ont exactement la même masse.

Lâcher les deux cônes simultanément d’une hauteur d’environ 2 m, le sommet dirigé vers le bas.

Ils atteignent tous les deux rapidement une vitesse de chute constante, leur vitesse limite, mais celle du cône le plus pointu est nettement plus grande que celle de l’autre.

Lorsqu’un objet a une vitesse v par rapport à l’air relativement grande (voir les remarques à ce propos), il subit de la part de l’air une force 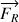appelée résistance de l’air de valeur :
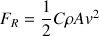(1)
(A : surface effective ou maître couple ; C : coefficient de pénétration dans l’air, caractéristique de la forme de l’objet).

La surface effective A est la surface de la projection de l’objet dans un plan perpendiculaire à la direction du mouvement. Lorsqu’un objet tombe dans l’air, sa vitesse augmente, donc la résistance qu’il subit de la part de l’air augmente. Lorsque la résistance de l’air atteint la même valeur que le poids, la vitesse reste constante, c’est la vitesse limite 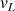telle que :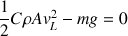

(m : masse de l’objet qui tombe ; g : intensité de la pesanteur).
D’où la vitesse limite :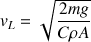
(2)

Le cône le plus aplati a une surface effective plus grande, donc il atteint une vitesse limite plus faible car les deux cônes ont exactement la même masse (ils ont été fabriqués à partir de la même quantité de papier).

Le nombre de Reynolds

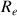
est un critère qui permet de déterminer si un écoulement est laminaire ou turbulent.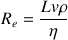

(L : dimension caractéristique de l’objet ; 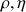: masse volumique et viscosité dynamique du fluide qui s’écoule ; v : vitesse d’écoulement).

Pour les faibles nombres de Reynolds

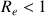
la force de frottement est donnée par la formule de Stokes pour une sphère dans un écoulement turbulent. Pour les écoulements turbulents
 
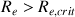
avec

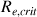
valeur particulière appelée valeur critique qui dépend de la forme de l’objet), la force de frottement est donnée par la formule (1). Les cônes qui tombent dans l’air subissent dès les très faibles vitesses un régime turbulent en raison de la très faible viscosité de l’air (η » 0,018 mPa.s).

Exemple numérique :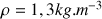
(masse volumique de l’air)
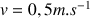(vitesse du cône)
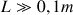(diamètre de la base du cône)
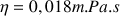(viscosité de l’air)
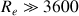(nombre de Reynolds de l’écoulement)