On peut créer un surplomb important en empilant des dominos.
Fiche d’accompagnement de l’expérience:

 Matériel
MatérielAu moins quatre objets identiques de forme parallélépipédique, par exemple des dominos.
 Montage et réalisation
Montage et réalisationVoici comment faire pour empiler des dominos les uns sur les autres, en créant un surplomb aussi important que possible.
Un premier domino est posé sur un support, son extrémité dépassant légèrement celui-ci.
Plaçer le deuxième domino en le décalant un peu par rapport au premier.
Et ainsi de suite avec les dominos suivants.
On peut réaliser facilement un empilage de quatre ou cinq dominos avant que la pile bascule.
Avec beaucoup de patience, on peut atteindre la trentaine ; le surplomb atteint alors le double de la longueur d’un domino.
L’expérience peut se faire avec tout objet de forme parallélépipédique, des livres par exemple.
Bien entendu, l’équilibre est de plus en plus précaire et il suffit d’une petite surcharge posée sur le dernier livre pour faire s’écrouler toute la pile.
 Explications
ExplicationsLe centre de gravité du premier domino est hors de la base de sustentation si moins de la moitié du domino est posée sur la table. Le domino subit alors un moment qui le fait basculer.
Le premier domino doit donc être posé de telle sorte que son centre de gravité se projette verticalement sur la table (voir la figure a). Lorsqu’on ajoute un deuxième domino sous le premier il faut que le centre de gravité de l’empilement soit à la verticale de la table (voir la figure b).
Le centre de gravité G123 de l’ensemble des 3 dominos est le barycentre du centre de gravité G12 de l’ensemble précédent de deux dominos affecté de la masse des deux dominos et du centre de gravité G3 du troisième domino affecté de la masse d’un domino (voir la figure c). La distance horizontale de G123 à G3 doit être le double de la distance horizontale de G123 à G12 et leur somme doit être égale à la demi-longueur L d’un domino.
La distance horizontale de G123 à G12 doit donc être
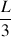 .
.
L’arête du troisième domino ne peut donc pas être à plus de
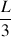
du bord de la table.
On calcule de la même façon que l’arête du quatrième domino ne peut pas être à plus de

du bord de la table (voir la figure d).
Pour N dominos, le surplomb total théorique est :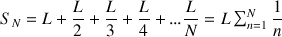
Cette série est divergente, on peut donc obtenir en théorie un surplomb aussi grand que l’on veut. Le tableau 1 donne la correspondance entre la taille du surplomb et le nombre de dominos à utiliser.
 Remarques
RemarquesOn peut faire une même expérience et un même calcul s’il s’agit de livres ou de briques.

